Lets Build the Reals.

The real numbers are probably what you think about when you think about numbers, but what are they? How do we get all those numbers from the ground up?

Von Neumann Ordinals

So we first want to create the naturals (and 0), and our tool to make these? Sets. However, we do have a problem, we don’t have anything to put in our set yet, so lets start by defining 0.

$0 := \{\}$

Now we have our first number defined we can start to inductively define the next numbers, given n, the successor of n, S(n) (Also known as n+1) is defined as

$S(n) := \{n, \{n\}\}$

And now we have defined all the natural numbers! With

$n := \{0,1,2,...,n-1\}$

So why do we define it this way?

There are other ways of defining the naturals, one could define

$S(n) := \{n\}$

This type of ordinals are called the Zermelo Ordinals, why are they not used? Well the reason is not that complex, its mostly down to the utility of the Von Neumann Ordinals, With Zermelo Ordinals, the cardinality (the number of elements in the set) is always one, however for Von Neumann Ordinals, the cardinality of a number is the number itself (in the way you’d normally understand it, not from the definition, that would be a bit circular), This means that we can say a set has a cardinality of n if there is a bijection from a set to n.

Now if we repeat the generative process above for all finite sets, this will give you the naturals and 0 $\mathbb{N}_0$ (or $\mathbb{N}$ We are going to be letting $0\notin\mathbb{N}$ ). Note you can extend these ordinals to transfinite size, this gives us $\omega$ with cardinality $\aleph_0$ , which you may have heard of.

Addition and multiplication

Now that we have the naturals (and 0) defined, lets define how to add and multiply numbers, as you’ve seen before we’ve already defined $n+1$ as $S(n)$ , so now we can inductively define $n+m$ as

$n+m := n + \underbrace{1 + 1 +... + 1}_{\text{$m$ times}}$

And now we can work on multiplication, we can also define that inductively with

$nm := n\times m := \underbrace{n + n + ... + n}_{\text{$m$ times}}$

With $n+0 := n$ and $n\times 0 := 0$

Now you may wonder why we don’t define subtraction and division yet, they are actually not that bad to define, we just say they are the inverses of addition and subtraction, however we cant define them yet as our current number systems are not closed under them, as $4-6\notin \mathbb{N}\cup\{0\}$ or $\frac{4}{3}\notin \mathbb{N}\cup\{0\}$

Time to get rational

Now that we have the naturals defined, lets start moving onto the rationals, you may wonder why we are not going onto the integers as they seem like the next step, they can actually be defined now, however the way they are defined is very similar to how we will define the reals from the positive reals later, the working here should not need that much editing to fit it here, but I personally think its nicer to stick with positive numbers (and 0) for now.

To define the rationals we need to first need to understand something called an equivalence class, so lets start there.

Equivalence Relations

We can define a relation $\sim$ as the subset of a set $X \times Y$ , think about it as question that takes in two inputs and gives you true or false about it (whether it is in $X \times Y$ or not), we write this as $x \sim y$ , pronounced as $x$ relates to $y$ , note that when $X = Y$ we call the relation homogeneous, we shall only use homogeneous relations from now on. One example of a relation would be $<$ on $\mathbb{N}$ so we could say $3<4$ but not $6<2$ or $1<1$

An equivalence relation is a specific type of relation that has various properties, these are

Reflexive, we can always say $x \sim x$
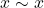
Symmetric, if we can say 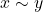$x \sim y$ , then we can always say that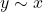 $y \sim x$
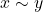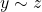Transitive, if we can say $x \sim y$ and $y \sim z$ , then we can always say that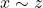 $x \sim z$

One example of an equivalence relation is that of birthdays, Clearly you have the same birthday as yourself, so it is reflexive, if you share a birthday with your twin, then your twin shares a birthday with your twin, so it is symmetric, and if your share a birthday with your twin, and your twin shares a birthday with me, then you share a birthday with me, so it is transitive.

Equivalence Classes

Let $~$ be an equivalence relation as defined above, on a set $X$ , lets now define the equivalence class, we define an equivalence class of an element $x$ , written as $\overline{x}$ and pronounced $x$ bar, is the set of items in $X$ which are equivalent to $x$ , in set notation one may write that as

$\overline{x} := \{ y \in X: x \sim y\}$

Now this does have some nice properties, if $y \in \overline{x}$ , then $\overline{y} = \overline{x}$ and if $y \notin \overline{x}$ , then $\overline{y} \cap \overline{x} = \emptyset$ ( $\emptyset$ is the empty set, also can be written as $\{\}$ ). These properties are actually quite nice to prove, and I’d recommend them if you want some simple statements to try and prove.

Using our birthday relation in the previous section, we can view the equivalence classes as the days of the year, as the members of each day would be those who share a birthday, and if two people did not share a birthday, then they would not be in the same class.

These classes are very useful for a lot of definitions, in fact you can define the previous ordinals in terms of these.

Now back to the rationals.

Now that we have equivalence classes defined, we can define the positive rationals, this is done by defining a relation on $\mathbb{N} \times \mathbb{N}$ buy $(p_1, q_1) \sim (p_2, q_2)$ if and only if $p_1 q_2 = p_2 q_1$ , Now that’s it, one can prove that this is in fact an equivalence relation (which you may want to try to do).

Now that we have this defined, we can now define the positive rationals as the equivalence classes of this relation. Doing this means that we can say that $(1, 4)$ and $(2, 8)$ are equal, so we can say that $\frac{1}{4} = \frac{2}{8}$ , you should note that while writing that I haven’t defined division yet, this however is not a problem, as when I write $\frac{1}{4}$ , I don’t mean $1$ divided by $4$ , I mean the number $0.25$ . Knowing this though we can actually define division now, as within the positive rationals, excluding $0$ , we can see that now given any two members of this set, dividing them gives a member of the set, so we can say that the positive rationals (excluding 0) is closed under the rationals.

Time for the positive reals

Now that we positive rationals and 0 defined (call this set $\mathbb{Q}_0$ , lets define the positive reals, we do this with something called Cauchy Sequences, there are other ways to define these, another method is called Dedekind Cut’s, however they both have their advantages and disadvantages.

So what is a sequence?

A sequence is a map from the naturals to the desired set, in this case $\mathbb{Q}_0$ , one can think of this as a list of numbers in order, for example one sequence could be

$\begin{aligned}a_0 &= 3.61231 \\a_1 &= 1.00002 \\a_2 &= 12 \\&\vdots \end{aligned}$

Convergence

Now that we have sequences defined, we need to know what it means for one to converge, so what does that mean? Well a sequence $(a_n)$ converges to $L$ if for any distance from the limit $L$ , called $\epsilon$ , then there is a point in the sequence, $N$ , such that for all values in the sequence that occur after $N$ , the distance from $L$ to the value is less than $\epsilon$ . This can be written formally as

$\forall \epsilon > 0, \exists N \in \mathbb{N}, \forall n \ge N, |a_n - L| < \epsilon$

But you don’t need to know what those symbols mean. Also, a Cauchy Sequence is another kind of sequence however it can be show that a sequence is Cauchy if and only if it is convergent, so we don’t need to bother with Cauchy sequences.

The Positive Reals

Now that we have the idea of a convergent sequence down, we can use this to define the reals, simply, given any sequence of numbers in $\mathbb{Q}_0$ that converges to a limit $L$ , then $L \in \mathbb{R}^+$

For example, we can see that $\pi \in \mathbb{R}^+$ , as we can see that the sequence

$\begin{aligned}a_0 &= 3 \\a_1 &= 3.1 \\a_2 &= 3.14 \\a_3 &= 3.141 \\a_4 &= 3.1415 \\a_5 &= 3.14159 \\&\vdots \end{aligned}$

converges to $\pi$ , so as all the elements of the sequence are rational, the sequence is one of rational numbers, so $\pi \in \mathbb{R}^+$

Now lets get Negative

Now that we have the positive rationals and 0, we can complete our number system by getting the negative reals, there are two ways we can do this, we could define another equivalence relation similar to the one we used to define the rationals, or we can construct two new sets one being $\mathbb{R}^+$ , and the other being $\mathbb{R}^-$ , we can define $\mathbb{R}^-$ as the ordered pair $(1, x)$ (here 1 is a flag telling us that the number is negative) such that for all $x \in \mathbb{R}^+$ and for all $y \in \mathbb{R}^-$ , $x > y$ , now we can define a map $\phi(x)$ from $\mathbb{R}^+$ to $\mathbb{R}^-$ by $\phi: x \mapsto (1,x)$ , now we can define the full reals as $\mathbb{R}^+ \cup \mathbb{R}^- \cup \{0\}$ now we can then define addition, subtraction, multiplication and division piecewise.

For example the negation of an item $x$ can be defined as

$-x = \begin{cases} \phi(x) & x\in \mathbb{R}^+ \\\phi^{-1}(x) & x\in \mathbb{R}^- \\0 & x = 0\end{cases}$

This method may seem more complex, but it does help to showcase a principle of the reals called trichotomy, which states that a number is either positive, negative or zero.